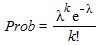The Poisson Distribution

The Poisson distribution began life with unusual applications.  It is a statistical function that is used to determine how many events of low probability will occur in a given time frame.  It is useful because only the average number of occurrences needs to be known.  From this, one can calculate the probability that the event will happen zero times in a given time interval, or fifty times.  λ is the expected number of occurrences in a time frame, and the probability that there will be exactly k occurrences of the phenomenon in a given time frame is given by the function on the right.

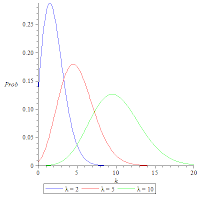Poisson Distribution for various values of λ

It's discoverer, Siméon-Denis Poisson (1781-1840), was a well-known French mathematician who worked in electrostatics and celestial mechanics.  He even got his name on the Eiffel Tower.  He had studied mathematics at the École Polytechnique in Paris starting in 1798 and became a professor there in 1802.  He had studied with the mathematicians Pierre-Simon Laplace (known for the Laplacian) and Joseph-Louis Lagrange (of Lagrange multipliers), and was a professor at the same time as André-Marie Ampère, known for his work in electromagnetism. His treatise introducing the Poisson distribution, however, bears the particularly unscientific title of Research on the Probability of Criminal and Civil Verdicts.¹ It was published in 1837, just three years before Poisson's death, and did not have a great impact at the time.

His distribution was brought to greater prominence by Ladislaus Josephovich Bortkiewicz (1868-1931), a Polish statistician.  In 1898 he published a book entitled, in English translation, The Law of Small Numbers, in which he showed that the Poisson distribution held for events even when the probabilities varied.  His examples were the number of men killed by horse kicks in the Prussian army over a 20 year period and the number of children who committed suicide in Prussia.  His work brought the Poisson distribution to a wider audience, and it is often called the Law of Small Numbers today.  As you can see, the Poisson distribution can be applied to many different situations, and some modern applications include the number of calls that a cell tower receives and the number of beds that an emergency room needs to have available.

[1] For a more detailed discussion of Poisson's work, see "A Study of Poisson's Models for Jury Verdicts in Criminal and Civil Trials" by Alan E. Gelfand and Herbert Solomon in the Journal of the American Statistical Association , Vol. 68, No. 342 (Jun., 1973), pp. 271-278.